[Resolução do Exercício 6. – Exame de Matemática 10ª Classe 2000 – 2ª Época] Considere as funções f(x)= (3/2)^x e g(x)=x+1. a) Indique o domínio de f. b) Represente f e g no mesmo S.C.O.
[Resolução do Exercício 6. – Exame de Matemática 10ª Classe 2000 – 2ª Época] Considere as funções f(x)= (3/2)^x e g(x)=x+1. a) Indique o domínio de f. b) Represente f e g no mesmo S.C.O.
[Resolução do Exercício 6. – Exame de Matemática 10ª Classe 2000 – 2ª Época] Considere as funções f(x)= (3/2)^x e g(x)=x+1. a) Indique o domínio de f. b) Represente f e g no mesmo S.C.O. c) Resolva: f(x) = g(x) em Z. d) Determine: f (2); e g(-1).
Tópicos deste Artigo
Togglea) Indique o domínio de f.
b) Represente f e g no mesmo S.C.O.
c) Resolva: f(x) = g(x) em Z.
d) Determine: f (2); e g(-1).
O domínio da função f(x) = (3/2)^x é todos os números reais, como qualquer número real pode ser elevado à potência de x. Isso significa que f(x) é definido para cada x no conjunto de números reais, que é denotado como R.
Para representar as funções f(x) = (3/2)^x e g(x) = x+1 no mesmo sistema de coordenadas, podemos usar os seguintes passos:
1. Escolha um intervalo de valores x para o domínio de f(x). Para este exemplo, podemos escolher valores x de -3 a 3.
2. Calcule os valores y correspondentes para f(x) usando a fórmula (3/2)^x.
3. Plote os pontos (x, f(x)) para cada x no intervalo escolhido.
1. Escolha um intervalo de valores x para o domínio de g(x). Para este exemplo, podemos escolher valores x de -3 a 3.
2. Calcule os valores y correspondentes para g(x) usando a fórmula x+1.
3. Plote os pontos (x, g(x)) para cada x no intervalo escolhido.
No mesmo sistema de coordenadas, plote ambos os conjuntos de pontos (f(x), x) e (g(x), x) para visualizar as funções f(x) e g(x) juntas.
![[Resolução do Exercício 6. - Exame de Matemática 10ª Classe 2000 – 2ª Época] Considere as funções f(x)= (3/2)^x e g(x)=x+1. a) Indique o domínio de f. b) Represente f e g no mesmo S.C.O. c) Resolva: f(x) = g(x) em Z. d) Determine: f (2); e g(-1).](https://exercicios.mozestuda.com/wp-content/uploads/2024/01/image-1024x932.png)
f(x) = (3/2)^x g(x) = x + 1
Estas são duas funções matemáticas que são dadas para serem iguais uma à outra quando x está no conjunto de inteiros, Z
Agora, precisamos resolver a equação f(x) = g(x) quando x é um inteiro.
f(x) = g(x) em Z pode ser escrito como: (3/2)^x = x + 1
Infelizmente, não há nenhuma formula algébrica simples conhecida para a equação (3/2)^x = x + 1 para x sendo um inteiro. No entanto, podemos usar métodos gráficos para encontrar os possíveis valores inteiros de x que satisfazem a equação.
Então, observando os gráficos representados na alínea b veremos que f(x) = g(x), isto e, os gráficos se encontram, nos pontos x=0 e x=4.
Então, f(x)=g(x) em x={0; 4}
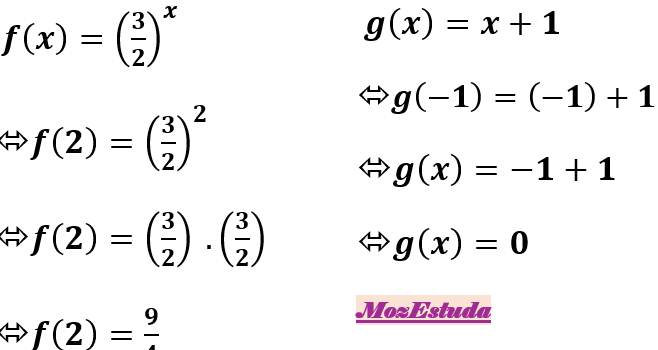





Seu trabalho académico de Matemática, Física, etc ... Projetos/Relatório está difícil?



Solicite Apoio Académico na Resolução dos seus trabalhos académicos: Projetos, TPC, Trabalhos de campo/ pesquisa, Testes Online, Cálculos/ Matemática …
Subscreva-se e fique dentro de todas atualizações
© 2024 MozEstuda Por: OSJ. Cumbe