Vamos resolver o problema com da função \( f(x) = 2x^2 – x \) no ponto \( x = -1 \): indicando a derivada por definição; a equação da reta tangente e construir gráfico do mesmo
Vamos resolver o problema com da função \( f(x) = 2x^2 – x \) no ponto \( x = -1 \): indicando a derivada por definição; a equação da reta tangente e construir gráfico do mesmo

ISCT – ALBERTO CHIPANDE – 1º TESTE DE MATEMÁTICA I – 2022
Exercício 1. Seja f(x) = 2x^2 − x no ponto x = −1
- a) Encontrar a derivada por definição
- b) Encontrar equação da recta tangente e constrói gráfico do mesmo
Vamos resolver o problema da função \( f(x) = 2x^2 – x \) no ponto \( x = -1 \): indicando a derivada por definição; a equação da reta tangente e construir gráfico do mesmo
Seja f(x) = 2x^2 − x no ponto x = −1
Tópicos deste Artigo
ToggleA derivada de \( f(x) \) no ponto \( x = a \) é dada por:
\[ f'(a) = \lim_{h \to 0} \frac{f(a + h) – f(a)}{h} \]
Para a função \( f(x) = 2x^2 – x \) no ponto \( x = -1 \):
1. Calcule \( f(a + h) \):
Substitua \( x \) por \( -1 + h \):
\[ f(-1 + h) = 2(-1 + h)^2 – (-1 + h) \]
2. Expanda \( f(-1 + h) \):
\[ (-1 + h)^2 = 1 – 2h + h^2 \]
\[ f(-1 + h) = 2(1 – 2h + h^2) – (-1 + h) \]
\[ = 2 – 4h + 2h^2 + 1 – h \]
\[ = 2h^2 – 5h + 3 \]
3. Calcule \( f(-1) \):
\[ f(-1) = 2(-1)^2 – (-1) = 2 + 1 = 3 \]
4. Substitua na fórmula da derivada:
\[ f'(-1) = \lim_{h \to 0} \frac{f(-1 + h) – f(-1)}{h} \]
\[ = \lim_{h \to 0} \frac{2h^2 – 5h + 3 – 3}{h} \]
\[ = \lim_{h \to 0} \frac{2h^2 – 5h}{h} \]
\[ = \lim_{h \to 0} (2h – 5) \]
5. Calcule o limite:
\[ f'(-1) = -5 \]
A equação da reta tangente a uma função \( f(x) \) no ponto \( x = a \) é dada por:
\[ y = f'(a)(x – a) + f(a) \]
Para \( f(x) = 2x^2 – x \) no ponto \( x = -1 \):
1. Derivada: \( f'(-1) = -5 \)
2. Valor da função no ponto: \( f(-1) = 3 \)
Então, a equação da reta tangente é:
\[ y = -5(x + 1) + 3 \]
\[ y = -5x – 5 + 3 \]
\[ y = -5x – 2 \]
Vamos construir o gráfico da função \( f(x) = 2x^2 – x \) e da reta tangente \( y = -5x – 2 \) no ponto \( x = -1 \).
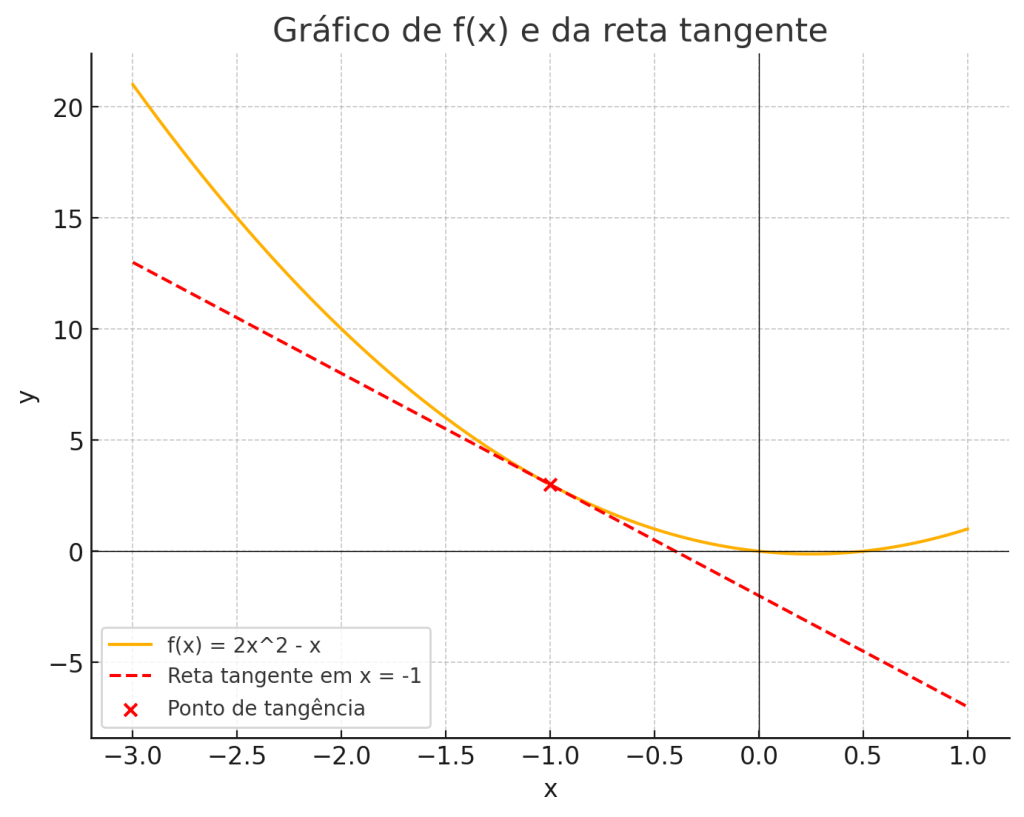
– A função \( f(x) \) está representada pela linha azul.
– A reta tangente \( y = -5x – 2 \) está representada pela linha tracejada vermelha.
– O ponto de tangência \( (-1, 3) \) está marcado com um ponto vermelho.
Resumo dos resultados:
– Derivada por definição: \( f'(-1) = -5 \)
– Equação da reta tangente: \( y = -5x – 2 \)





Seu trabalho académico de Matemática, Física, etc ... Projetos/Relatório está difícil?



Solicite Apoio Académico na Resolução dos seus trabalhos académicos: Projetos, TPC, Trabalhos de campo/ pesquisa, Testes Online, Cálculos/ Matemática …
Subscreva-se e fique dentro de todas atualizações
© 2024 MozEstuda Por: OSJ. Cumbe