Resolução do Exame de Matemática 10ª classe (2019) – 1ª Época

Exame de Matemática 10ª classe (2019) – 1ª Chamada

Resolução do Exame de Matemática 10ª classe (2019) – 1ª Época

Exercício 1.

Com os símbolos \( \in, \notin, \subset, \subseteq \) ou \( \not\subseteq \), complete na sua folha de respostas de modo a obter afirmações verdadeiras:

a) \( \{0;1\};… [0;[ \) 

Resposta: \( \{0;1\} \subseteq [0;1[ \) 

(Os elementos \( 0 \) e \( 1 \) estão contidos no intervalo \( [0;1[ \), mas \( 1 \notin [0;1[ \), então \( \subseteq \) é a relação correta).

b) \( -3… \mathbb{Q} \) 

Resposta: \( -3 \in \mathbb{Q} \) 

(O número \( -3 \) é racional, logo pertence ao conjunto dos números racionais \( \mathbb{Q} \)).

c) \( 1,435… \mathbb{N} \) 

Resposta: \( 1,435 \notin \mathbb{N} \) 

(O número \( 1,435 \) não é um número natural, logo não pertence ao conjunto \( \mathbb{N} \)).

d) \( \mathbb{R}_0^+ \cap \mathbb{R}_0^- … \{0\} \) 

Resposta: \( \mathbb{R}_0^+ \cap \mathbb{R}_0^- = \{0\} \) 

(A interseção entre os números reais não negativos \( \mathbb{R}_0^+ \) e os números reais não positivos \( \mathbb{R}_0^- \) contém apenas o número \( 0 \)).

—

Exercício 2.

 2. Classifique em verdadeiro (V) ou falso (F):

a) Dois planos distintos, paralelos, têm um ponto comum. 

Resposta: Falso. Planos paralelos distintos não se cruzam e, portanto, não têm pontos em comum.

b) Se uma reta é paralela a dois planos, então esses planos são paralelos. 

Resposta: Falso. Uma reta pode ser paralela a dois planos sem que os dois planos sejam paralelos entre si.

c) Se duas retas são ortogonais, então elas formam um ângulo reto. 

Resposta: Verdadeiro. Retas ortogonais são perpendiculares, formando um ângulo reto.

d) Se duas retas são perpendiculares, então elas formam um ângulo reto. 

Resposta: Verdadeiro. Por definição, retas perpendiculares formam um ângulo de \( 90^\circ \).

—

Exercício 3.

 3. Resolva:

a) \( 2 \sin x = \sqrt{2}, \, \text{para} \, x \in [0^\circ;90^\circ] \) 

Resposta: Dividindo ambos os lados por 2, temos: 

\[\sin x = \frac{\sqrt{2}}{2}\]

Sabemos que \( \sin 45^\circ = \frac{\sqrt{2}}{2} \), logo: 

\( x = 45^\circ \).

b) \( \log_5(2x+1) – \log_5 x = 0 \) 

Resposta: Aplicando a propriedade dos logaritmos, temos:\[\log_5\left(\frac{2x+1}{x}\right) = 0\]

Logo, \( \frac{2x+1}{x} = 5^0 = 1 \), e resolvendo a equação:

\[2x + 1 = x \implies x = -1\]

—

Exercício 4.

 4. Dada a equação \( x^2 – 4x + (5 – m) = 0 \), determine \( m \) de modo que a equação admita duas raízes reais de sinais contrários.

Resposta: Para que as raízes sejam reais e de sinais contrários, o discriminante \( \Delta \) deve ser positivo, e o produto das raízes deve ser negativo.

O discriminante é:

\[\Delta = b^2 – 4ac = (-4)^2 – 4(1)(5 – m) = 16 – 4(5 – m) = 4m – 4\]

Para que as raízes sejam reais, \( \Delta > 0 \):

\[4m – 4 > 0 \implies m > 1\]

Além disso, o produto das raízes deve ser negativo, ou seja:

\[5 – m < 0 \implies m > 5\]

Portanto, \( m > 5 \).

—

Exercício 5.

 5. Resolva em \( \mathbb{R} \):

\( x^4 – 4x^2 = 0 \)

Resposta: Fatorando a equação:

\[x^2(x^2 – 4) = 0 \implies x^2(x – 2)(x + 2) = 0\]

Logo, as soluções são:

\[x = 0, \, x = 2, \, x = -2\]

—

Exercício 6.

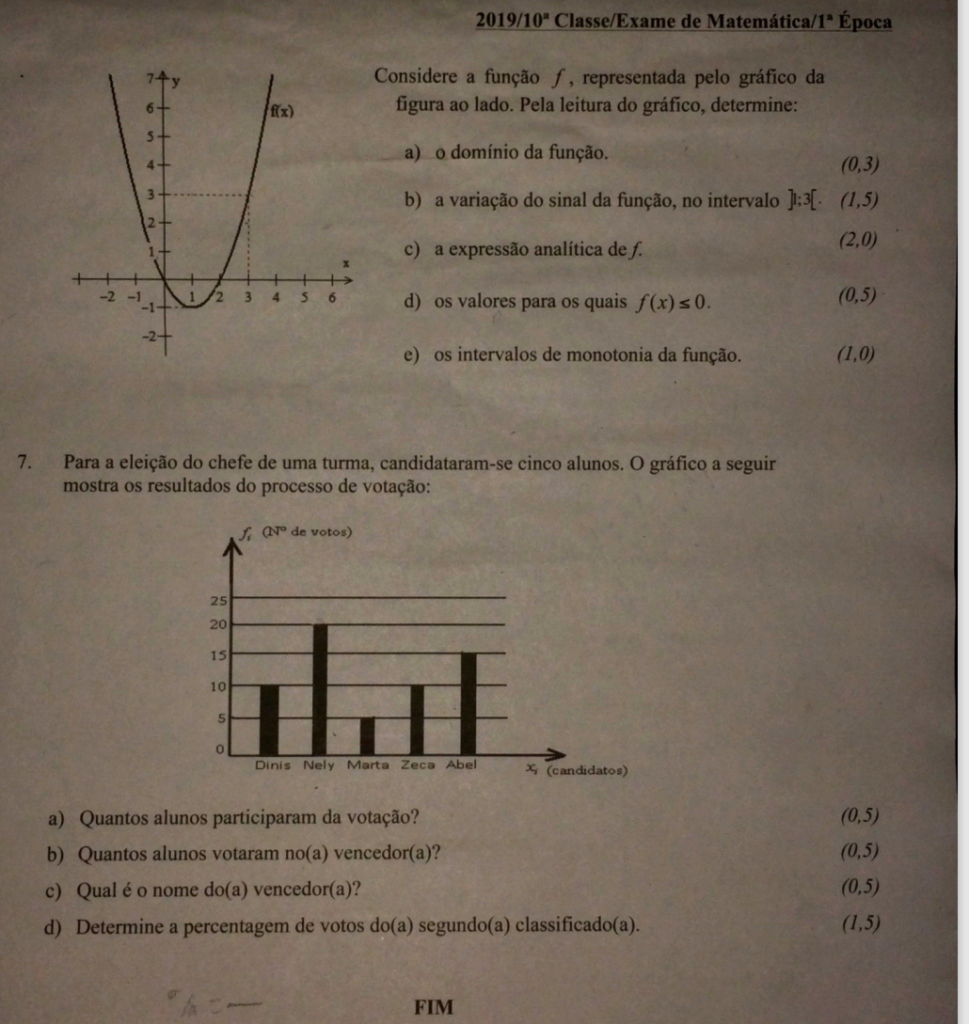
 6. Considere a função \( f \), representada pelo gráfico da figura ao lado. Pela leitura do gráfico, determine:

a) O domínio da função. 

Resposta: O domínio é o conjunto de todos os valores de \( x \) para os quais a função está definida. 

\[D(f) = \mathbb{R}\]

b) A variação do sinal da função, no intervalo \( ]-3;6[ \). 

Resposta: A função é negativa no intervalo \( x \in ]-3;1[ \) e positiva no intervalo \( x \in ]1;6[ \).

c) A expressão analítica de \( f \). 

Resposta: Sem a fórmula exata ou pontos específicos, a função parece ser uma parábola do tipo \( f(x) = ax^2 + bx + c \).

d) Os valores para os quais \( f(x) \leq 0 \). 

Resposta: A função é menor ou igual a zero no intervalo:

\[x \in [-3;1]\]

e) Os intervalos de monotonia da função. 

Resposta: A função é decrescente em \( x \in [-3;1] \) e crescente em \( x \in [1;6] \).

—

Exercício 7.

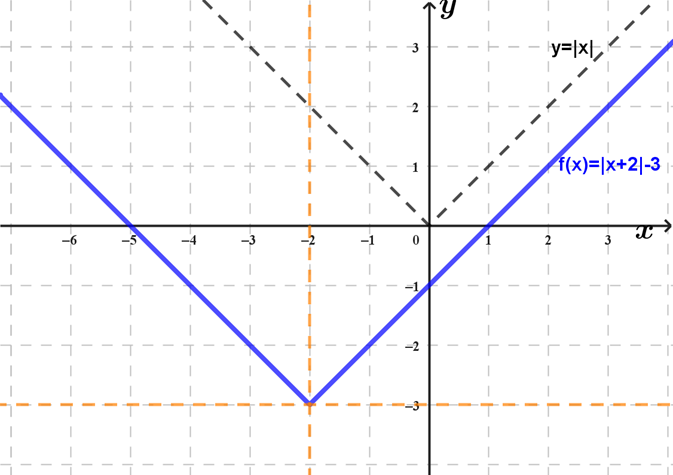
 7. Para a eleição do chefe de uma turma, candidataram-se cinco alunos. O gráfico a seguir mostra os resultados do processo de votação:

Os valores de votos são: \( Dinis = 10 \), \( Nely = 20 \), \( Marta = 5 \), \( Zeca = 10 \), \( Abel = 15 \).

a) Quantos alunos participaram da votação? 

Resposta: O total de alunos que participaram é a soma dos votos: 

\[10 + 20 + 5 + 10 + 15 = 60\]

b) Quantos alunos votaram no(a) vencedor(a)? 

Resposta: O vencedor foi Nely, com 20 votos.

c) Qual é o nome do(a) vencedor(a)? 

Resposta: Nely.

d) Determine a percentagem de votos do(a) segundo(a) classificado(a). 

Resposta: O segundo classificado foi Abel, com 15 votos. A percentagem de votos foi:

\[\frac{15}{60} \times 100 = 25\%\]